Suppose P is the initial amount (which is lent, deposited, invested or principal), t is the time or tenure & r is rate of interest, then Simple Interest (SI) can be calculated as below:

From the above formula, Principal (P), Rate (r) & Time (t) can be calculated as follows:

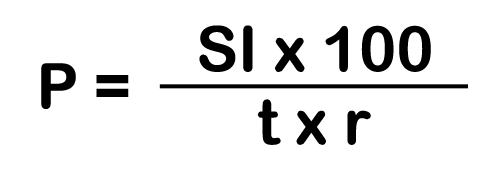
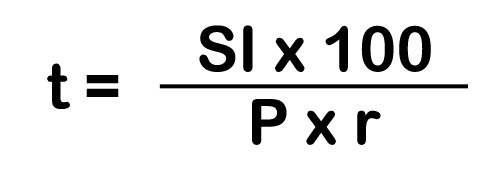
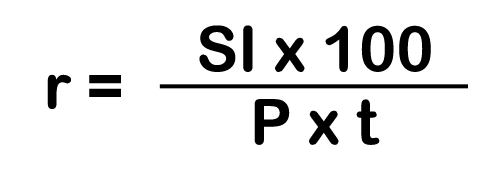
And, final Amount (A) can be calculated as:

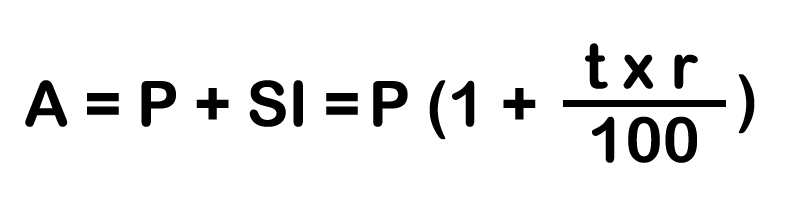
Example:

Suppose a certain sum of money is deposited at 5% per annum Simple Interest, which amounted to Rs. 50,000 after 10 years. Then the sum of money can be calculated by the following:

Amount = A = Rs. 50,000

Rate = r = 5

Time = t = 10

Therefore, Principal = P = the sum of money = A/(1+((t x r)/100)) = 50000/(1+((10 x 5)/100)) = 50000/(1+(5/10)) = (50000 x 10)/15 = Rs. 33,333.33

and. Simple Interest = SI = A-P = 50000 – 33333.33 = Rs. 16,666.67