Upstream:
Boat is moving against the direction of water.
Suppose, u is the speed of boat in still water & v is the speed of stream, then:
Upstream Speed (x) = (u-v)km/hr
Downstream:
Boat is moving along the direction of water.
Suppose, u is the speed of boat in still water & v is the speed of stream, then:
Downstream Speed (y) = (u+v)km/hr
Speed Of Boat In Still Water:
0.5(y+x)
Speed Of Stream:
0.5(y-x)
Suppose, u is the upstream speed, v is the downstream speed and w is the speed of boat in still water. Then:

Suppose a boat takes n hours to travel from 1 point to another and back to the same point, where u is the speed of boat in still water & v is the speed of stream. Then:

Suppose a boat takes n1 hours to travel a distance and n2 hours to return the same distance, where v is the speed of stream. Then:
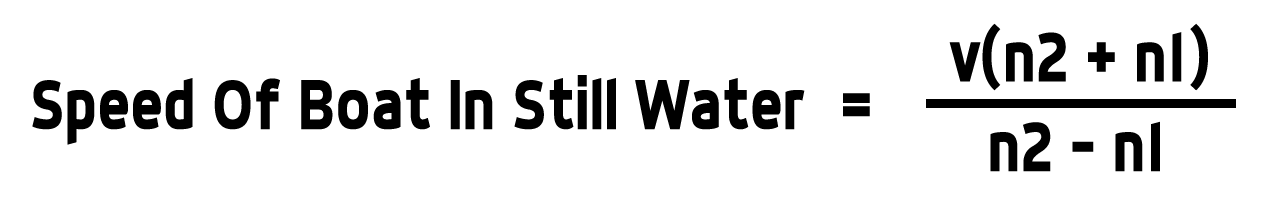
Suppose a boat takes n hours more, in case of upstream, than downstream, u is the speed of boat in still water and v is the speed of stream. Then:

